The simulations below illustrate a discretization algorithm that automatically translates the "continuum approximation" (CA) recipes for facility location problems into discrete designs. They apply to transshipment terminal systems but can also be used for other logistics problems. The procedure outperforms conventional methods for large problems. For more background information, see Ouyang and Daganzo (2003).
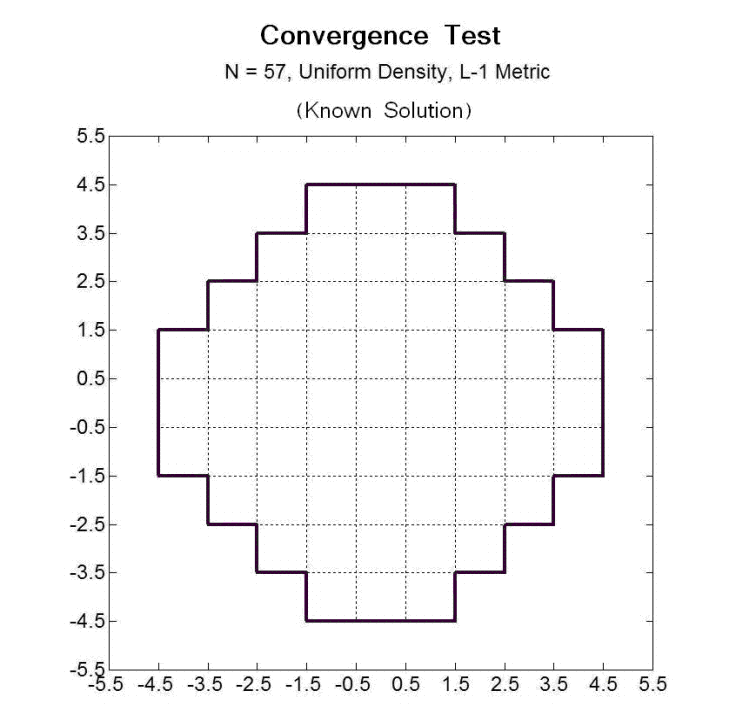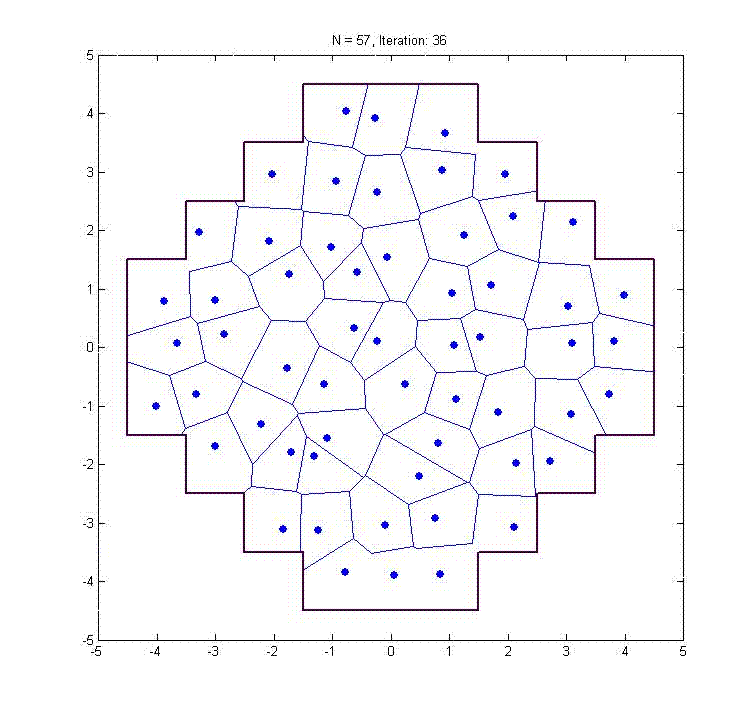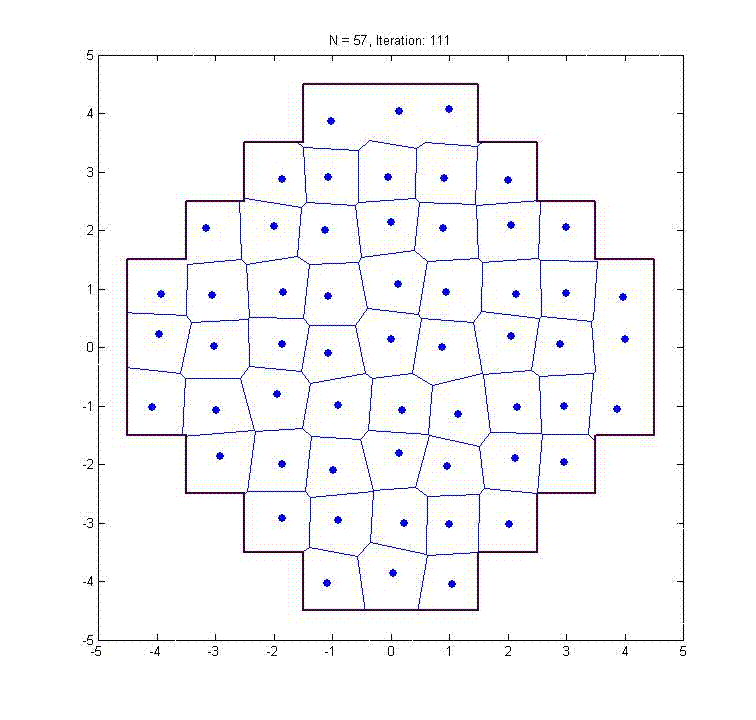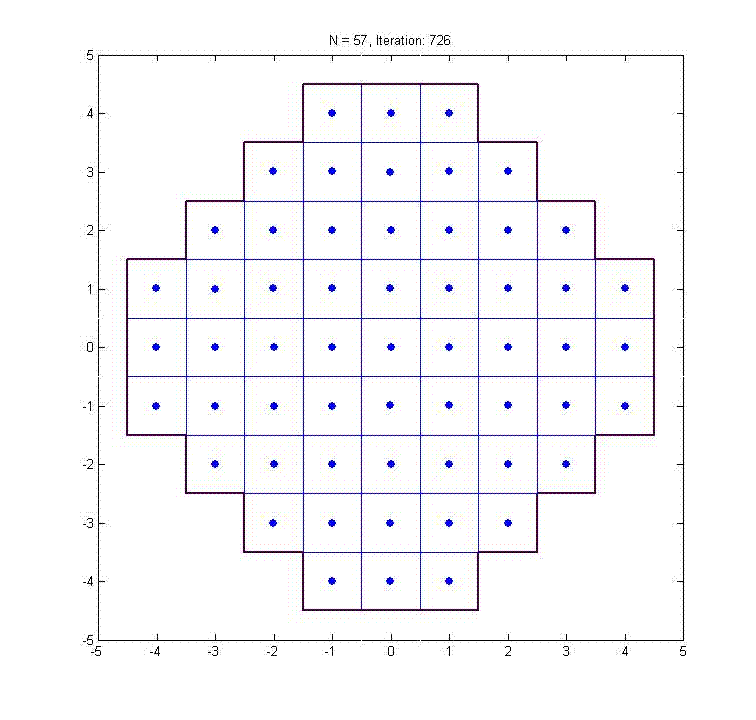
This animation shows how the method finds the optimal locations of 57 terminals over the region you see. We assume for this example that the goal is to minimize the average (Manhattan) distance from a point in the region to the nearest terminal. The optimal locations are known to be at the centers of the 57 identical squares that make up the region.

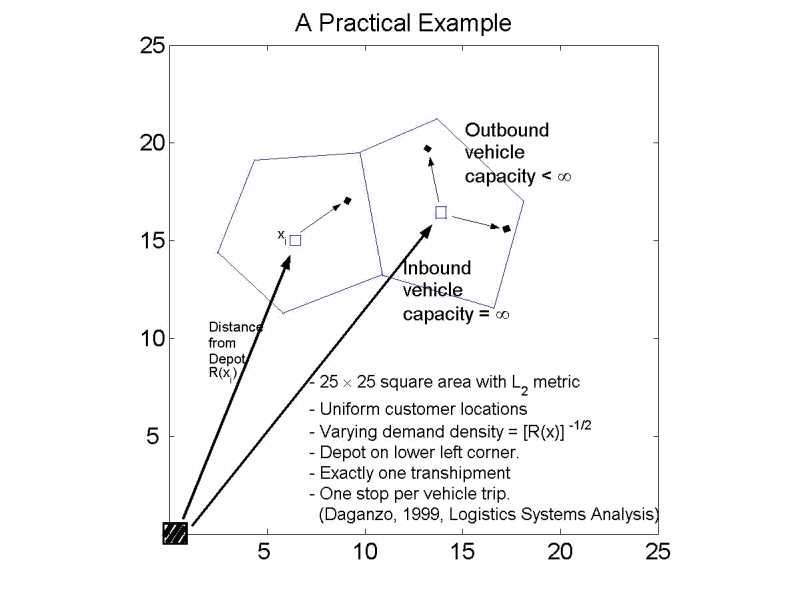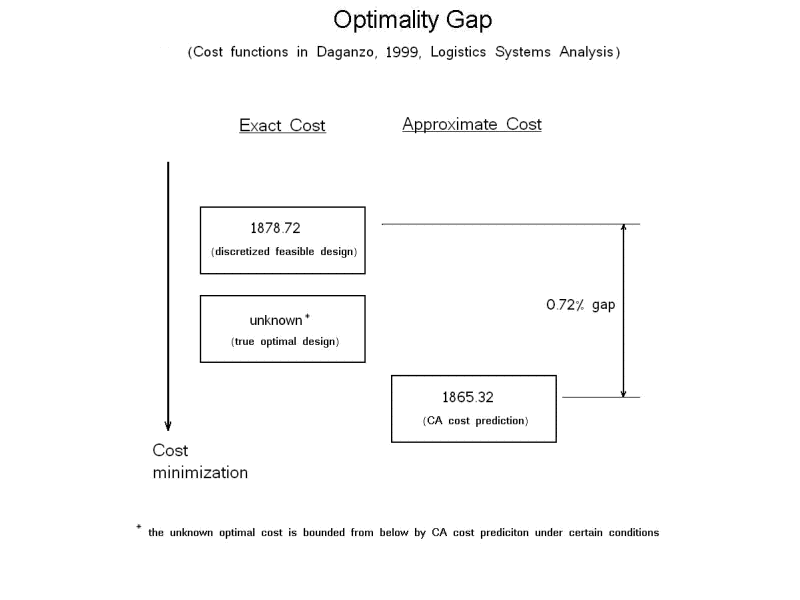
Customers are uniformly located in a 25×25 square area S. Demand decreases with the distance from a depot at one corner of S. Service is provided from a depot with transshipments at intermediate terminals. Vehicles with large capacity shuttle between the depot and the terminals. Small-capacity vehicles provide local delivery from the terminals. The goal here is minimizing logistics costs with the optimal number of terminals, locations and service regions. The animation shows how the simulated CA procedure finds a solution when transportation costs are evaluated with Euclidean distances. The display beneath, gives more details; for a complete explanation see Ouyang and Daganzo (2003).