Slope Stability

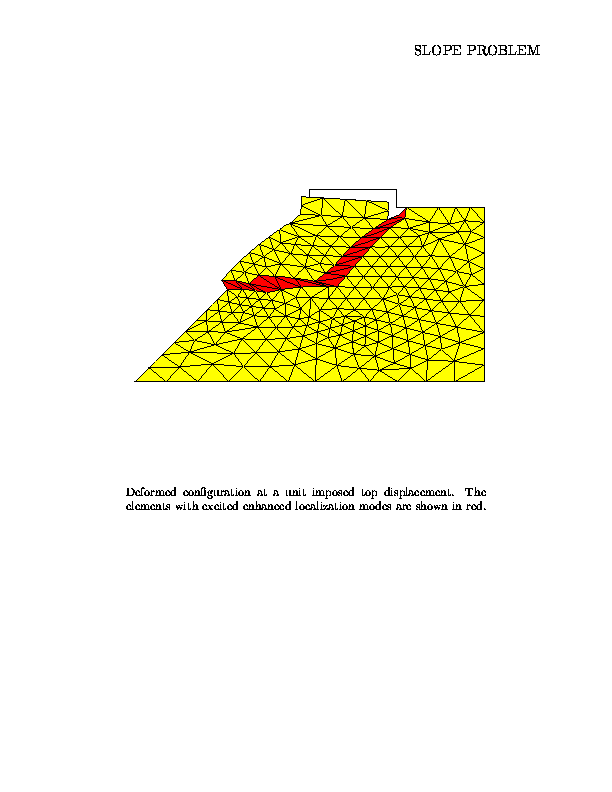
Description:

Finite element simulation of the stability of a slope in plane strain. The material is modeled with a finite strain plasticity model based on the multiplicative decomposition of the deformation gradient (F = FeFp). The von Mises yield criteria with isotropic strain-softening is assumed. A rigorous analysis of the model in the context of distribution theory identifies the formation of strong discontinuities ( discontinuities in the displacement field) in the material. In addition, the softening response is shown to be localized along the discontinuity. Enhanced finite element methods are designed to capture the corresponding singular strain field. The resulting formulation resolves correctly the localized dissipation along the failure surface, leading to numerical solutions independent of the mesh size and mesh alignment.

References:

J.C. Simo, J. Oliver and F. Armero [1993] ``An Analysis of Strong Discontinuities Induced by Strain-Softening in Rate Independent Inelastic Solids" Computational Mechanics, 12, 277-296.

F. Armero and K. Garikipati [1995] ``Recent Advances in the Analysis and Numerical Simulation of Strain Localization in Inelastic Solids" Proceed. Computational Plasticity - COMPLAS IV, ed. by D.R.J. Owen, E. Onate and E. Hinton, Barcelona, 547-563.

F. Armero and K. Garikipati [1995] An Analysis of Strong Discontinuities in Multiplicative Finite Strain Plasticity and their Relation with the Numerical Simulation of Strain Localization in Solids" International Journal of Solids and Structures, 33, 2863-2885.

F. Armero [1999], ``Large-Scale Modeling of Localized Dissipative Mechanisms in a Local Continuum: Applications to the Numerical Simulation of Strain Localization in Rate-Dependent Inelastic Models," Journal of the Mechanics of Cohesive-Frictional Materials, 4, 101-132.

F. Armero [1998], ``On the Characterization of Localized Solutions in Inelastic Solids: An Analysis of Wave Propagation in a Softening Bar," submitted to Computer Methods in Applied Mechanics and Engineering (available also as Report no. UCB/SEMM-97/18, UC Berkeley).