Conserving Algorithms for Dynamic Contact Problems

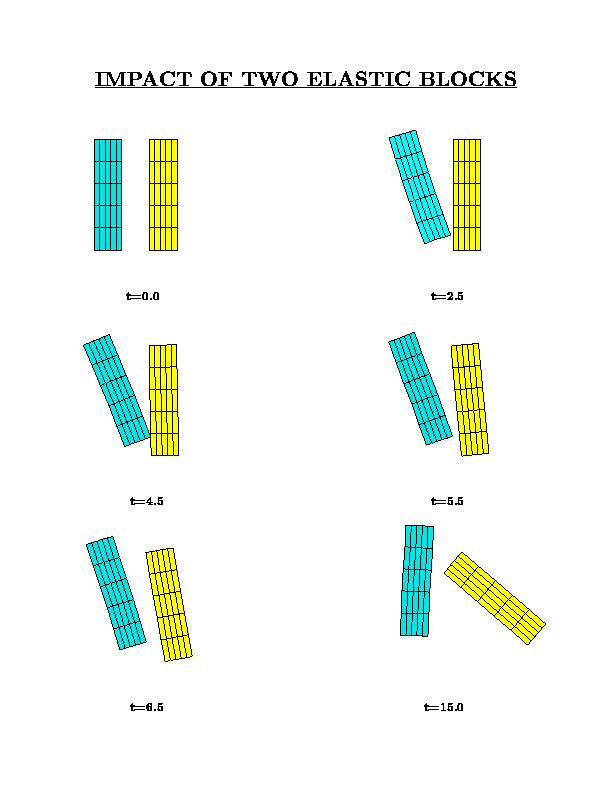
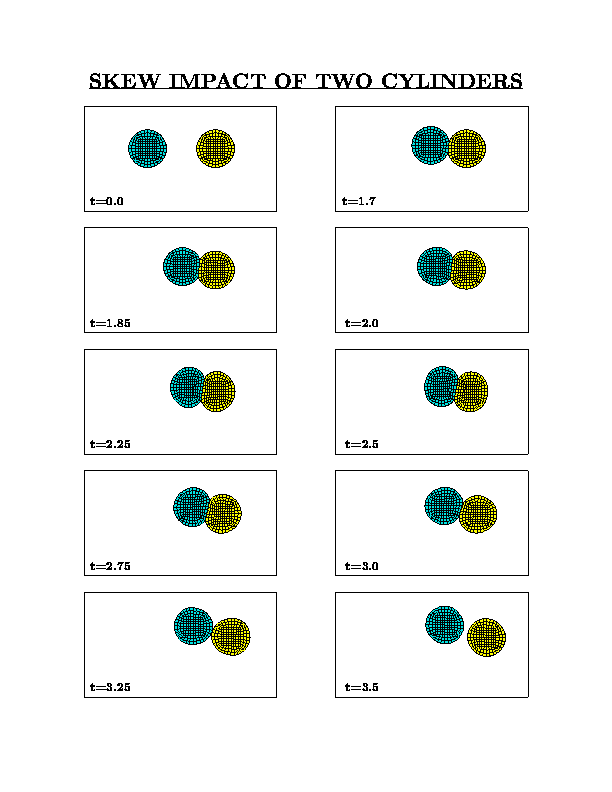
Description:

The frictionless contact/impact of two free elastic bodies is characterized by full energy, linear and angular momenta conservation. It is then of the main interest that the numerical schemes exhibit the same conservation laws. From a purely numerical point of view, the conservation of energy is particularly important by the added numerical stability of the computer simulations.

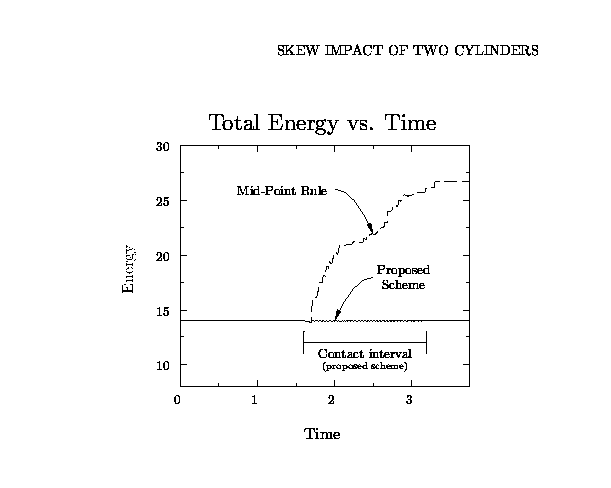
The figures below show the results obtained with a new class of conserving algorithms for dynamic contact problems. The impact of two elastic blocks and two cylinders is considered, with the blue solids impacting the yellow solids which are at rest. The numerical scheme is based on a penalty regularization of the contact constraints with complete control of the total energy in the system. During contact, energy is stored in the penalty potentials, leading to no energy increase as compared with more traditional schemes (mid-point and trapezoidal rules), and thus to superior stability properties. Furthermore, full energy conservation is accomplished upon release. The linear and angular momenta are conserved at all times. The scheme imposes the gap contraints both in the displacement and velocity, resulting in a more stable enforcement of these constraints when compared to standard schemes.

We have also developed extensions of thiee algorithms for the integration of the tangential frictional interactions between solids. In this case, the algorithms do preserve the diissipative physical character of these interactions in contrast with exisitng schemes. The final algorithms result in stable powerful techniques for the solution of multi-body systems.

References:

F. Armero and E. Petocz [1998], ``Formulation and Analysis of Conserving Algorithms for Dynamic Contact/Impact Problems," Computer Methods in Applied Mechanics and Engineering, 158, 269-300.

F. Armero and E. Petocz [1999], ``A New Dissipative Time-Stepping Algorithm for Frictional Contact Problems: Fromulation and Analysis," Computer Methods in Applied Mechanics and Engineering, 179, 151-178.

F. Armero and E. Petocz [1997] ``On the Formulation of Stable Time-Stepping Algorithms for Contact Problems," Proc. Computational Plasticity Conf., COMPLAS V, ed. by D.R.J Owen, E. Onate and E. Hinton, Barcelona, 1997.

F. Armero and E. Petocz [1996] ``A New Class of Conserving Algorithms for Dynamic Contact Problems" ECCOMAS'96, Paris, John Wiley & Sons, 861-867.